Launch
Risk is an interesting game, powered by simple mathematics. In the battle, the attacker throws three dice, the defender throws two. The attacker's advantage is the one extra die. The defender's advantage is that he/she wins when the dice are tied. Which, in the general situation of 3 dice vs. 2 dice roll, translates into the following odds: the attacker has 37.17% chance of winning, the defender has 33.58% chance of winning, and there's a 29.26 % chance of tie - they will both lose one army. But what about specific situations? How can I know if my 10 armies are enough against my opponent's 5+4?
Since I'm a developer and not a mathematician, I decided I will rather build a simple brute force JavaScript simulator than try to derive the formula behind the battles. An application that simulates 10.000 Risk fights (around 50.000 dice rolls) and calculates the result odds. That should be enough to make an approximation, right?
Risk's rules specify that the attacker always has to leave one army behind (can't use it to attack), and can attack any number of territories in a single turn. Which the calculator also takes into account. Every territory the attacker wins, his/her number of armies is subtracted by 1 (one army is left behind), and the last army is not able to attack. I think I got it right, but if you find and error, please let me know.
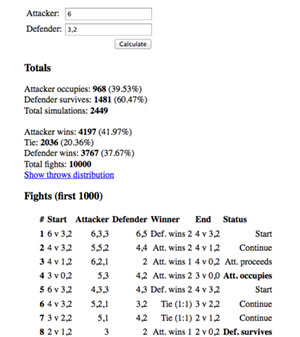
Risk dice roll battle simulation.
Besides, the simulator also knows how to calculate probabilities for specific single battle situations for different numbers of dice the attacker and defender throw, by going through all the possibilities of dice throw results (which means 7.776 (65) different dice throws in 3 vs. 2 battle).
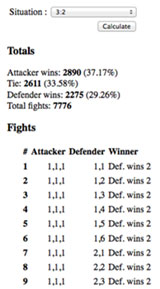
Risk dice roll possibilities and odds.
I made this to help myself and others understand and appreciate the statistics behind the dice. So, the next time you play Risk, don't forget to bring your phone and use the simulator to your unfair advantage. And if you're a developer, feel free to upgrade the algorithm (available on Github). Game on.
http://diceroll.stritar.net/risk.html
https://github.com/gstritar/DiceRoll