Everybody that owns an aquarium probably came across this decision at one point. The water is filthy and needs to be replaced. All you have is a jar. And you ask yourself: should you be emptying the aquarium first, adding new water later on, or should you be replacing filthy water with clean water? The first choice seems more rational, but sometimes you can't fully empty the aquarium (e.g. you have fish), and you need to do more runs since you're not taking water both ways. The other option seems interesting since you're efficient both ways, but at the same time you're taking back fresh water mixed in the aquarium. So, what should you do?
The situation
In reality, you do have other options. A water pump, a larger intermediate basin or other things that can make this task easier. But believe me, sometimes you don't have the time to do it properly and you just want to clean the water a bit. And that's when you'll wonder what to do. It happened to me, and that's why I've made myself a model that would answer this question, a model that would determine the breaking point (where both options are equally effective) between the two techniques.
The model described contains the following parameters:
- the aquarium volume (V - volume)
- the jar volume (d - change)
- number of two-way runs (x)
And it looks something like this:
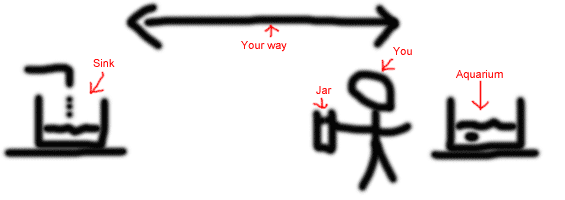
The aquarium cleaning situation
The initial model
The original view I made in Excel is based on simple mathematics, where each one-way run is represented by one line in the table. Adding and removing water both-ways constantly reduces filthiness, but makes each additional run less effective. On the other hand, removing water first and adding fresh water later takes more runs (since your jar is empty in one direction, you require four one-way runs to replace an additional unit), but you're not removing clean water. Here's a preview of how this looks:
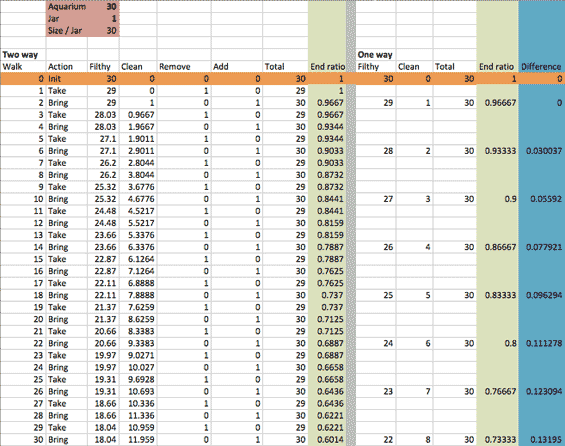
The basic calculation
The advanced model
The basic model is more understandable, but not appropriate to make a full mathematical equation. That's why I made a second model, which is based on two-way runs and exponential functions. Here's what I got:
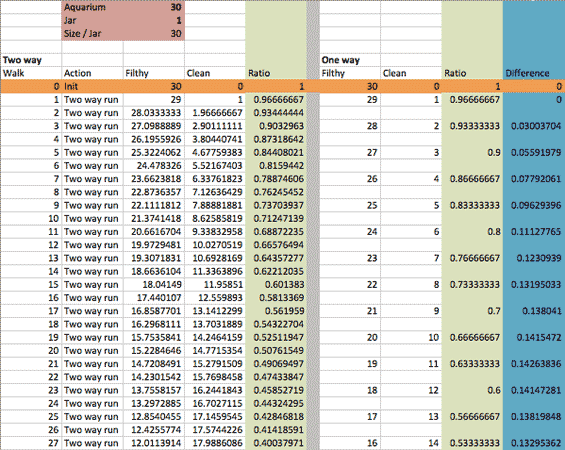
The advanced calculation
The results
The results show that if you don't have much time, it's better if you're replacing water, taking it both ways. This accounts for faster cleaning, which is slowing down in the long run. But the point is that no matter what the parameters are (aquarium and jar size), the breaking point happens more to the end of the cleaning. So, if you're not prepared to fully empty the aquarium, it's generally better if you use the the first option, removing and adding water at the same time.
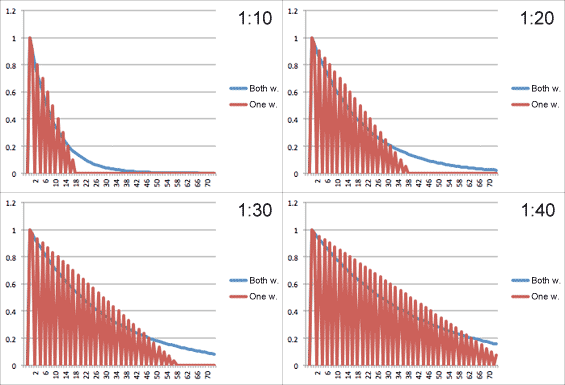
The graphical results displaying water filthiness based on number of two-way runs for different jar and aquarium sizes
The breaking point equation
The results are there, and I managed to make the following equation which would calculate where both ways are the equally effective:
This makes calculating the number of runs so complex it can't be calculated in basic Excel (because of the Lambert W or product log function).
But luckily, you can use Wolfram Alpha to calculate the breaking point of two-way runs by entering the aquarium and jar size in the boxes below. If you're prepared to make less two-way runs than the result, take water both-ways, otherwise, one-way.
Aquarium: Jar:
If you want to play around a bit, you can even download the complete model in Excel format.
Conclusion
Perhaps there's an easier way to calculate the great aquarium cleaning dilemma, which speaks in favor of water replacement (taking water both ways). There's also a chance I've made an error somewhere (please let me know!). But the results seem correct, and I hope you find all of this amusing and / or helpful when you need to update your water. Aquarium cleaning will never be the same again.
Update (26.11.2011): While this may have been a fun experiment, I've just read it's not that smart to fully remove water in the aquarium, since it disrupts the balance of bacteria.